ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░: č乊čĆą╝čāą╗ą░. ąŚą░čłč鹊 čśąĄ ą┐ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮą░ ąĖ čāą┐ąĖčüą░ąĮą░ čā ą║ą▓ą░ą┤čĆą░čé čśąĄą┤ąĮą░ą║ą░ ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą╝ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą╝ čéčĆąŠčāą│ą╗čā, ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą╝, čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą╝ čéčĆą░ą┐ąĄąĘčā?
ąÜą░ą║ąŠ ą┐čĆąŠąĮą░čøąĖ ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░? ą¤čĆą▓ąŠ ą┐čĆąŠąĮą░čÆąĖč鹥 čĆą░ą┤ąĖčśčāčü. ąØą░čāčćąĖč鹥 ą┤ą░ čĆąĄčłą░ą▓ą░č鹥 čśąĄą┤ąĮąŠčüčéą░ą▓ąĮąĄ ąĖ čüą╗ąŠąČąĄąĮąĄ ąĘą░ą┤ą░čéą║ąĄ.
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░: č乊čĆą╝čāą╗ą░ ą║čĆąŠąĘ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║, ą┐čĆąĄčćąĮąĖą║, ą┤čāąČąĖąĮčā ą║čĆčāą│ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║čĆąŠąĘ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║:
- ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ-ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║čĆąŠąĘ ąö-ą┐čĆąĄčćąĮąĖą║:
- ąØą░ą╗ą░ąČąĄčÜąĄ ąĪ ą║čĆčāą│ą░ ą░ą║ąŠ čśąĄ ą┐ąŠąĘąĮą░čéą░ ą┤čāąČąĖąĮą░ ą║čĆčāą│ą░:
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čé: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ąŚą░ą┤ą░čéą░ą║ ą▒čĆ. 1: ąĪčéčĆą░ąĮąĖčåą░ ą║ą▓ą░ą┤čĆą░čéąĮąĄ čäąĖą│čāčĆąĄ, ą║ąŠčśą░ čśąĄ čśąĄą┤ąĮą░ą║ąŠ 6 čåąĄąĮčéąĖą╝ąĄčéą░čĆą░, ą┐ąŠąĘąĮą░č鹊 čśąĄ. ą¤čĆąŠąĮą░čÆąĖč鹥 ąĪ-ą┐ąŠą▓čĆčłąĖąĮčā čāą┐ąĖčüą░ąĮąŠą│ ą║čĆčāą│ą░.
- ąŚą░ą┤ą░čéą░ą║ #2: ąØą░čøąĖ ąĪ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čéąĮčā čäąĖą│čāčĆčā ąĖ čÜąĄą│ąŠą▓ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║, ą░ą║ąŠ čśąĄ čśąĄą┤ąĮą░ čüčéčĆą░ąĮąĖčåą░ čśąĄą┤ąĮą░ą║ą░ ą░=4 čåą╝.
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮąŠą│ ąŠą║ąŠ ą║ą▓ą░ą┤čĆą░čéą░: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą╗ąĖ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆąŠčāą│ą░ąŠ: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāąČąĮąĖčåąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą│ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą│ čéčĆąŠčāą│ą╗ą░: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą░ąŠąĮąĖ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆą░ą┐ąĄąĘ: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāąČąĮąĖčåąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą░ ą┐čĆą░ą▓ąŠčāą│ą░ąŠąĮąĖ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆą░ą┐ąĄąĘ: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
- ąÆąĖą┤ąĄąŠ: ą£ą░č鹥ą╝ą░čéąĖą║ą░ | ąĀą░čćčāąĮą░čÜąĄ ą┐ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ ąĖ čÜąĄą│ąŠą▓ąĖčģ ą┤ąĄą╗ąŠą▓ą░
ąÜčĆčāą│ čśąĄ ąĘą░čéą▓ąŠčĆąĄąĮą░ ą║čĆąĖą▓ą░. ąæąĖą╗ąŠ ą║ąŠčśą░ čéą░čćą║ą░ ąĮą░ ą║čĆčāąČąĮąŠčś ą╗ąĖąĮąĖčśąĖ ą▒ąĖčøąĄ čśąĄą┤ąĮą░ą║ąŠ čāą┤ą░čÖąĄąĮą░ ąŠą┤ čåąĄąĮčéčĆą░ą╗ąĮąĄ čéą░čćą║ąĄ. ąÜčĆčāą│ čśąĄ čĆą░ą▓ą░ąĮ ąŠą▒ą╗ąĖą║, ą┐ą░ čśąĄ čĆąĄčłą░ą▓ą░čÜąĄ ąĘą░ą┤ą░čéą║ą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜą░ ą┐ąŠą▓čĆčłąĖąĮąĄ čśąĄą┤ąĮąŠčüčéą░ą▓ąĮąŠ. ąŻ ąŠą▓ąŠą╝ čćą╗ą░ąĮą║čā čøąĄą╝ąŠ čĆą░ąĘą╝ąŠčéčĆąĖčéąĖ ą║ą░ą║ąŠ ą┐čĆąŠąĮą░čøąĖ ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā čéčĆąŠčāą│ą░ąŠ, čéčĆą░ą┐ąĄąĘ, ą║ą▓ą░ą┤čĆą░čé ąĖ ąŠą┐ąĖčüą░ąĮčā čā ą▒ą╗ąĖąĘąĖąĮąĖ ąŠą▓ąĖčģ čäąĖą│čāčĆą░.
ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░: č乊čĆą╝čāą╗ą░ ą┐ąŠą╝ąŠčøčā ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ą░, ą┐čĆąĄčćąĮąĖą║ą░, ą┤čāąČąĖąĮąĄ ą║čĆčāą│ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ą┐čĆąŠą▒ą╗ąĄą╝ą░
ąöą░ ą▒ąĖčüč鹥 ą┐čĆąŠąĮą░čłą╗ąĖ ą┐ąŠą▓čĆčłąĖąĮčā čäąĖą│čāčĆą░, ą╝ąŠčĆą░č鹥 ąĘąĮą░čéąĖ ą┤ą░ čśąĄ čéą░ą║ą░ą▓ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║, ą┐čĆąĄčćąĮąĖą║ ąĖ ą▒čĆąŠčś ŽĆ.
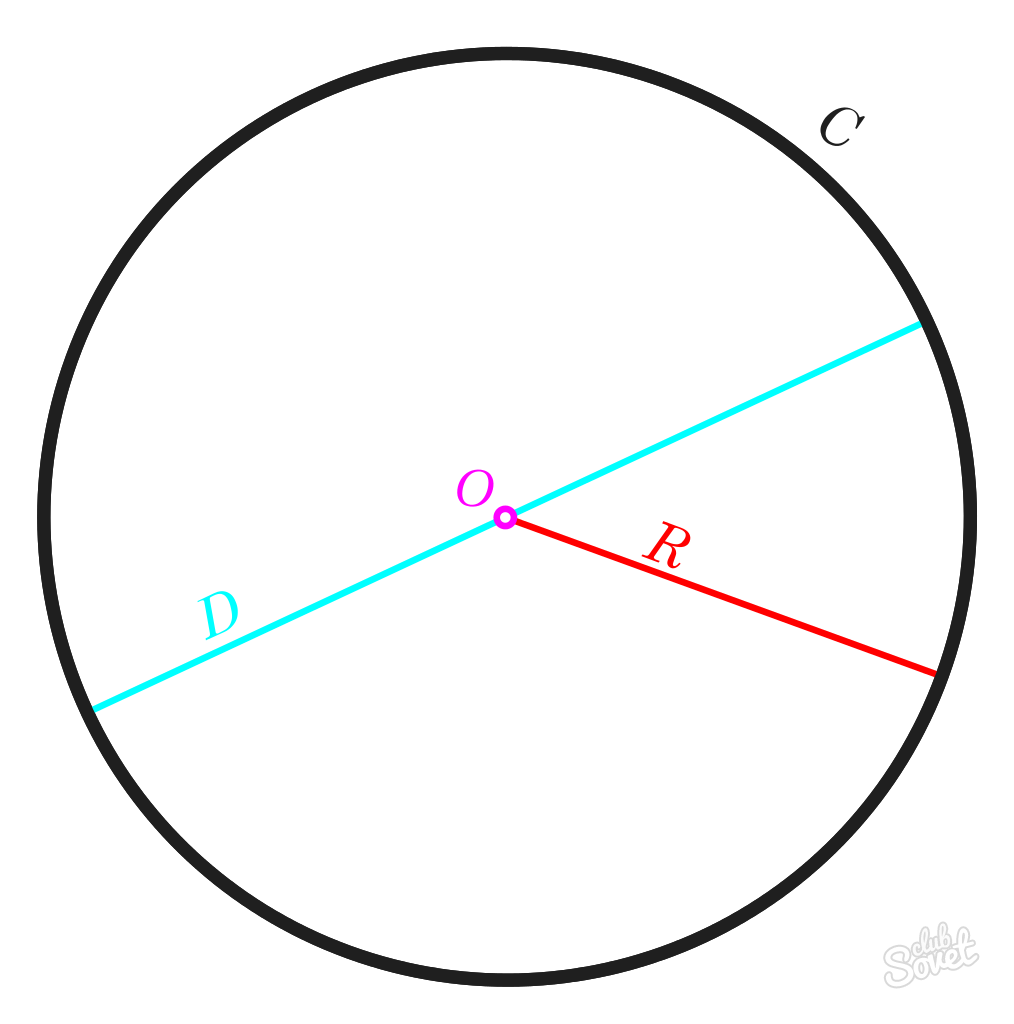
ą¤ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ąĀ čśąĄ čĆą░čüč鹊蜹░čÜąĄ ąŠą│čĆą░ąĮąĖč湥ąĮąŠ čåąĄąĮčéčĆąŠą╝ ą║čĆčāąČąĮąĖčåąĄ. ąöčāąČąĖąĮąĄ čüą▓ąĖčģ ąĀ-čĆą░ą┤ąĖčśčāčüą░ čśąĄą┤ąĮąŠą│ ą║čĆčāą│ą░ ą▒ąĖčøąĄ čśąĄą┤ąĮą░ą║ąĄ.
ą¤čĆąĄčćąĮąĖą║ ąö čśąĄ ą╗ąĖąĮąĖčśą░ ąĖąĘą╝ąĄčÆčā ą▒ąĖą╗ąŠ ą║ąŠčśąĄ ą┤ą▓ąĄ čéą░čćą║ąĄ ąĮą░ ą║čĆčāąČąĮąĖčåąĖ ą║ąŠčśą░ ą┐čĆąŠą╗ą░ąĘąĖ ą║čĆąŠąĘ čåąĄąĮčéčĆą░ą╗ąĮčā čéą░čćą║čā. ąöčāąČąĖąĮą░ ąŠą▓ąŠą│ čüąĄą│ą╝ąĄąĮčéą░ čśąĄ čśąĄą┤ąĮą░ą║ą░ ą┤čāąČąĖąĮąĖ ąĀ-čĆą░ą┤ąĖčśčāčüą░ ą┐ąŠą╝ąĮąŠąČąĄąĮąŠą│ čüą░ 2.
ąæčĆąŠčś ŽĆ čśąĄ ą║ąŠąĮčüčéą░ąĮčéąĮą░ ą▓čĆąĄą┤ąĮąŠčüčé čśąĄą┤ąĮą░ą║ą░ 3,1415926. ąŻ ą╝ą░č鹥ą╝ą░čéąĖčåąĖ čüąĄ ąŠą▓ą░čś ą▒čĆąŠčś ąŠą▒ąĖčćąĮąŠ ąĘą░ąŠą║čĆčāąČčāčśąĄ ąĮą░ 3,14.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║čĆąŠąĘ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║:
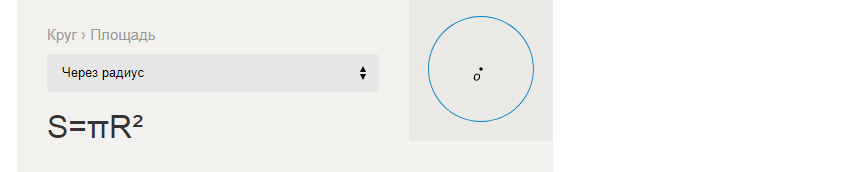
ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ-ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║čĆąŠąĘ ąĀ-čĆą░ą┤ąĖčśčāčü:
---------- ---------------------------- --
ąŚą░ą┤ą░čéą░ą║: ąØą░čÆąĖč鹥 ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░, ą░ą║ąŠ čśąĄ čÜąĄą│ąŠą▓ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ 7 čåą╝.
ąĀąĄčłąĄčÜąĄ: ąĪ=ŽĆąĀ2, ąĪ=3,14*72, ąĪ=3,14*49=153,86 čåą╝2.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čśąĄ 153,86 čåą╝2.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ-ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║čĆąŠąĘ ąö-ą┐čĆąĄčćąĮąĖą║:

ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ ą░ą║ąŠ čśąĄ ąö ą┐ąŠąĘąĮą░č鹊:
--------- --------------------------------
ą£ąĖčüąĖčśą░: ą¤čĆąŠąĮą░čÆąĖč鹥 ąĪ ą║čĆčāą│ą░, ą░ą║ąŠ čśąĄ čÜąĄą│ąŠą▓ąŠ ąö čśąĄą┤ąĮą░ą║ąŠ 10 čåą╝.
ąĀąĄčłąĄčÜąĄ: ą¤=ŽĆ*ą┤2/4, ą¤=3,14*102/4=3,14*100/4=314/4=78,5 čåą╝2.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą▓čĆčłąĖąĮą░ čĆą░ą▓ąĮąĄ ąŠą║čĆčāą│ą╗ąĄ čäąĖą│čāčĆąĄ čśąĄ 78,5 čåą╝2.
ą¤čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ ą║čĆčāą│ą░, ą░ą║ąŠ čśąĄ ą┐ąŠąĘąĮą░čéą░ ą┤čāąČąĖąĮą░ ą║čĆčāą│ą░:
ą¤čĆą▓ąŠ, ąĮą░ą╗ą░ąĘąĖą╝ąŠ ą║ąŠą╗ąĖą║ąĖ čśąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║. ąöčāąČąĖąĮą░ ą║čĆčāą│ą░ čüąĄ ąĖąĘčĆą░čćčāąĮą░ą▓ą░ ą┐ąŠ č乊čĆą╝čāą╗ąĖ: ąø=2ŽĆąĀ, čüčģąŠą┤ąĮąŠ č鹊ą╝ąĄ, čĆą░ą┤ąĖčśčāčü ąĀ čøąĄ ą▒ąĖčéąĖ čśąĄą┤ąĮą░ą║ ąø/2ŽĆ. ąĪą░ą┤ą░ ąĮą░ą╗ą░ąĘąĖą╝ąŠ ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░ ą║ąŠčĆąĖčüč鹥čøąĖ č乊čĆą╝čāą╗čā ą║čĆąŠąĘ ąĀ.
ąĀą░ąĘą╝ąŠčéčĆąĖą╝ąŠ čĆąĄčłąĄčÜąĄ ąĮą░ ą┐čĆąĖą╝ąĄčĆčā ąĘą░ą┤ą░čéą║ą░:
----------- ----------------------------
ąŚą░ą┤ą░čéą░ą║: ąØą░čÆąĖč鹥 ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░, ą░ą║ąŠ čśąĄ ą┐ąŠąĘąĮą░čéą░ ą┤čāąČąĖąĮą░ ą║čĆčāą│ą░ ąø ŌĆö 12 čåą╝.
ąĀąĄčłąĄčÜąĄ: ą¤čĆą▓ąŠ ąĮą░ą╗ą░ąĘąĖą╝ąŠ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║: ąĀ=ąø/2ŽĆ=12/2*3,14=12/6,28=1,91.
ąĪą░ą┤ą░ ąĮą░ą╗ą░ąĘąĖą╝ąŠ ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆąŠąĘ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║: ąĪ=ŽĆąĀ2=3,14*1,912=3,14*3,65=11,46 čåą╝2.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čśąĄ 11,46 čåą╝2.
ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čé: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
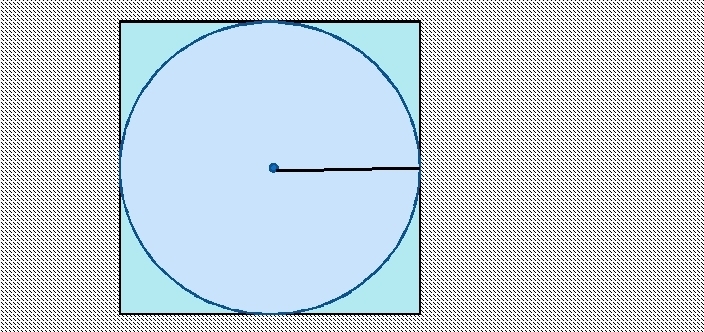
ą¤čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čé čśąĄ čśąĄą┤ąĮąŠčüčéą░ą▓ąĮąŠ. ąĪčéčĆą░ąĮą░ ą║ą▓ą░ą┤čĆą░čéą░ čśąĄ ą┐čĆąĄčćąĮąĖą║ ą║čĆčāą│ą░. ąöą░ ą▒ąĖčüč鹥 ą┐čĆąŠąĮą░čłą╗ąĖ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║, ą┐ąŠčéčĆąĄą▒ąĮąŠ čśąĄ ą┤ą░ ą┐ąŠą┤ąĄą╗ąĖč鹥 čüčéčĆą░ąĮčā čüą░ 2.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čé:

ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čé:
-- ---------------------------------- ----
ąŚą░ą┤ą░čéą░ą║ ą▒čĆąŠčś 1: ą¤ąŠąĘąĮą░čéą░ čśąĄ čüčéčĆą░ąĮąĖčåą░ ą║ą▓ą░ą┤čĆą░čéąĮąĄ čäąĖą│čāčĆąĄ ą║ąŠčśą░ čśąĄ čśąĄą┤ąĮą░ą║ą░ 6 čåąĄąĮčéąĖą╝ąĄčéą░čĆą░. ą¤čĆąŠąĮą░čÆąĖč鹥 ąĪ-ą┐ąŠą▓čĆčłąĖąĮčā čāą┐ąĖčüą░ąĮąŠą│ ą║čĆčāą│ą░.
ąĀąĄčłąĄčÜąĄ: ąĪ=ŽĆ(ą░/2)2=3,14(6/2)2=3,14*9=28,26 čåą╝2.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą▓čĆčłąĖąĮą░ čĆą░ą▓ąĮąĄ ąŠą║čĆčāą│ą╗ąĄ čäąĖą│čāčĆąĄ čśąĄ 28,26 čåą╝2.
-------------------------------------------------- -----------
ąŚą░ą┤ą░čéą░ą║ #2 :ą¤čĆąŠąĮą░čÆąĖč鹥 ąĪ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą║ą▓ą░ą┤čĆą░čéąĮčā čäąĖą│čāčĆčā ąĖ čÜąĄą│ąŠą▓ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ą░ą║ąŠ čśąĄ čśąĄą┤ąĮą░ čüčéčĆą░ąĮą░ čśąĄą┤ąĮą░ą║ą░ ą░=4 ą▓ąĖą┤ąĖ
ąĀąĄčłąĖč鹥 ąĮą░ čüą╗ąĄą┤ąĄčøąĖ ąĮą░čćąĖąĮ : ą¤čĆą▓ąŠ ąĮą░ą╗ą░ąĘąĖą╝ąŠ ąĀ=ą░/2=4/2=2 ą▓ąĖą┤ąĖ
ąĪą░ą┤ą░ čøąĄą╝ąŠ ąĮą░čøąĖ ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░ ąĪ=3,14*22=3,14*4=12,56 čåą╝2.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą▓čĆčłąĖąĮą░ čĆą░ą▓ąĮąĄ ą║čĆčāąČąĮąĄ čäąĖą│čāčĆąĄ čśąĄ 12,56 čåą╝2.
ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮąŠą│ ąŠą║ąŠ ą║ą▓ą░ą┤čĆą░čéą░: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
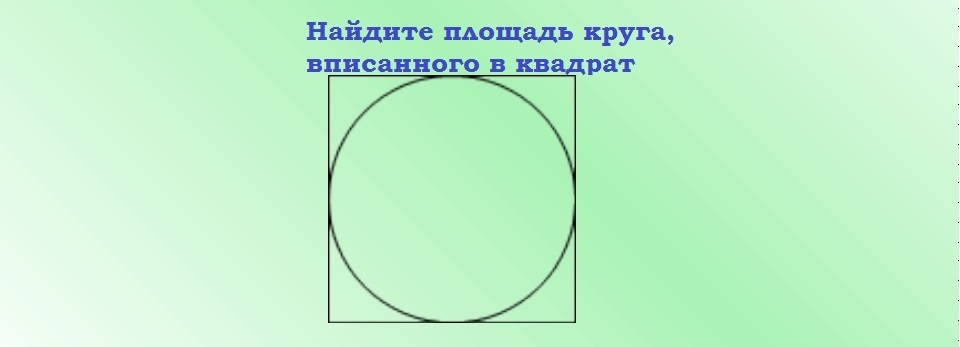
ą£ą░ą╗ąŠ čśąĄ č鹥ąČąĄ ą┐čĆąŠąĮą░čøąĖ ą┐ąŠą▓čĆčłąĖąĮčā ąŠą║čĆčāą│ą╗ąĄ čäąĖą│čāčĆąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą║ą▓ą░ą┤čĆą░čéą░. ąÉą╗ąĖ, ąĘąĮą░čśčāčøąĖ č乊čĆą╝čāą╗čā, ą╝ąŠąČąĄč鹥 ą▒čƹʹŠ ąĖąĘčĆą░čćčāąĮą░čéąĖ ąŠą▓čā ą▓čĆąĄą┤ąĮąŠčüčé.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ąĪ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮąŠą│ ąŠą║ąŠ ą║ą▓ą░ą┤čĆą░čéąĮąĄ čäąĖą│čāčĆąĄ:

ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮąŠą│ ąŠą║ąŠ ą║ą▓ą░ą┤čĆą░čéąĮąĄ čäąĖą│čāčĆąĄ:
ąŚą░ą┤ą░čéą░ą║

ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą░ąŠ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆąŠčāą│ą░ąŠ: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
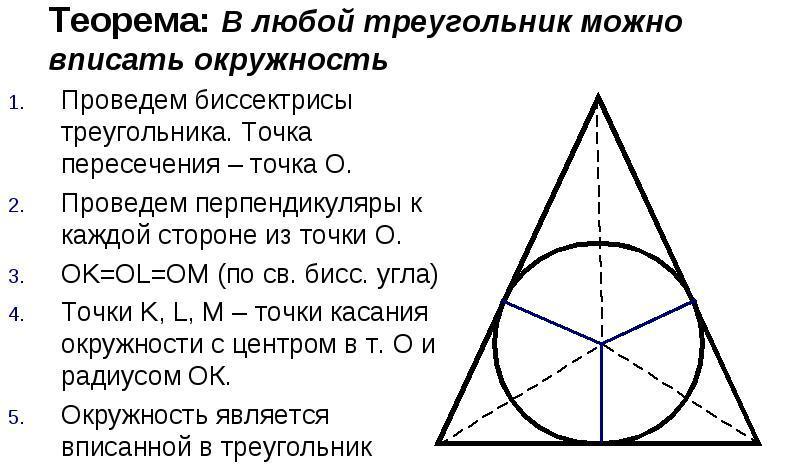
ąÜčĆčāą│ čāą┐ąĖčüą░ąĮ čā čéčĆąŠčāą│ą╗ą░čüčéčā čäąĖą│čāčĆčā čśąĄ ą║čĆčāąČąĮąĖčåą░ ą║ąŠčśą░ ą┤ąŠą┤ąĖčĆčāčśąĄ čüą▓ąĄ čéčĆąĖ čüčéčĆą░ąĮąĄ čéčĆąŠčāą│ą╗ą░. ąæąĖą╗ąŠ ą║ąŠčśą░ čéčĆąŠčāą│ą╗ą░čüčéą░ čäąĖą│čāčĆą░ ą╝ąŠąČąĄ ą▒ąĖčéąĖ čāą┐ąĖčüą░ąĮą░ ą║čĆčāą│ąŠą╝, ą░ą╗ąĖ čüą░ą╝ąŠ čśąĄą┤ąĮąŠą╝. ą”ąĄąĮčéą░čĆ ą║čĆčāą│ą░ čøąĄ ą▒ąĖčéąĖ čéą░čćą║ą░ ą┐čĆąĄčüąĄą║ą░ čüąĖą╝ąĄčéčĆą░ą╗ą░ čāą│ą╗ą░ čéčĆąŠčāą│ą╗ą░.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆąŠčāą│ą░ąŠ:
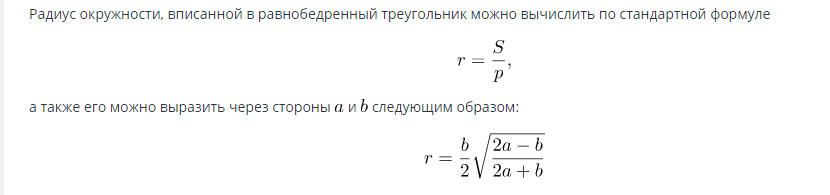
ąÜą░ą┤ą░ čśąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ą┐ąŠąĘąĮą░čé, ą┐ąŠą▓čĆčłąĖąĮą░ čüąĄ ą╝ąŠąČąĄ ąĖąĘčĆą░čćčāąĮą░čéąĖ ą┐ąŠą╝ąŠčøčā č乊čĆą╝čāą╗ąĄ: ąĪ=ŽĆąĀ2.
ążąŠčĆą╝čāą╗ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą╗ąĖ čéčĆąŠčāą│ą░ąŠ:
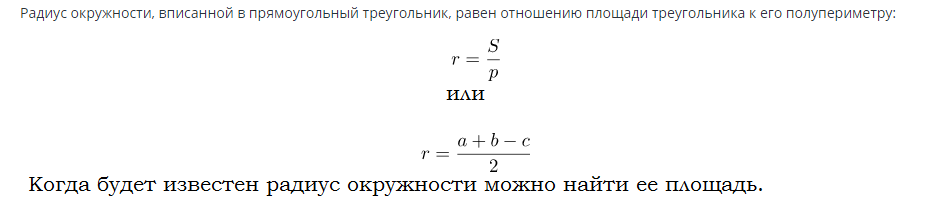
ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłąĄčÜą░ ą┐čĆąŠą▒ą╗ąĄą╝ą░:
ąŚą░ą┤ą░čéą░ą║ ą▒čĆ. 1
 )
)ąÉą║ąŠ čā ąŠą▓ąŠą╝ ąĘą░ą┤ą░čéą║čā čéą░ą║ąŠčÆąĄ čéčĆąĄą▒ą░ ą┤ą░ ą┐čĆąŠąĮą░čÆąĄč鹥 ą┐ąŠą▓čĆčłąĖąĮčā ą║čĆčāą│ą░ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ą░ 4 čåą╝, ąŠąĮą┤ą░ č鹊 ą╝ąŠąČąĄč鹥 čāčćąĖąĮąĖčéąĖ ą┐ąŠ č乊čĆą╝čāą╗ąĖ: ąĪ=ŽĆąĀ2
ąŚą░ą┤ą░čéą░ą║ #2
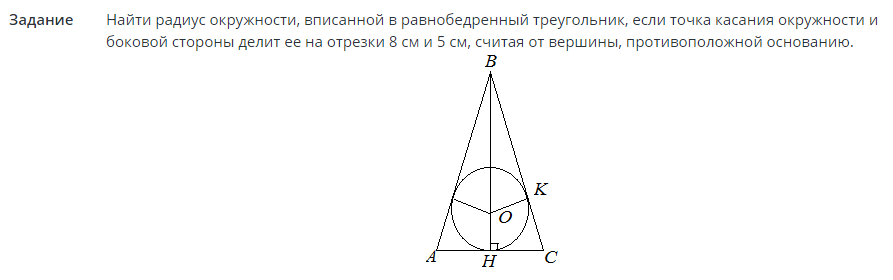
ąĀąĄčłąĄčÜą░:

ąĪą░ą┤ą░ ą║ą░ą┤ą░ čśąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ą┐ąŠąĘąĮą░čé, ą┐ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čüąĄ ą╝ąŠąČąĄ ąĮą░čøąĖ čā čüą╝ąĖčüą╗čā čĆą░ą┤ąĖčśčāčüą░. ą¤ąŠą│ą╗ąĄą┤ą░čśč鹥 č乊čĆą╝čāą╗čā ąĖąĘąĮą░ą┤ čā č鹥ą║čüčéčā.
ąŚą░ą┤ą░čéą░ą║ #3

ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāąČąĮąĖčåąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą│ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą│ čéčĆąŠčāą│ą╗ą░: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░
ąĪą▓ąĄ č乊čĆą╝čāą╗ąĄ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čüą▓ąŠą┤ąĖ čüąĄ ąĮą░ čćąĖčÜąĄąĮąĖčåčā ą┤ą░ ą┐čĆą▓ąŠ ą╝ąŠčĆą░č鹥 ą┐čĆąŠąĮą░čøąĖ čÜąĄą│ąŠą▓ čĆą░ą┤ąĖčśčāčü. ąÜą░ą┤ą░ čśąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ą┐ąŠąĘąĮą░čé, ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ čśąĄ čśąĄą┤ąĮąŠčüčéą░ą▓ąĮąŠ, ą║ą░ąŠ čłč鹊 čśąĄ ą│ąŠčĆąĄ ąŠą┐ąĖčüą░ąĮąŠ.
ŌĆŗŌĆŗą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāąČąĮąĖčåąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą│ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą│ čéčĆąŠčāą│ą╗ą░ ąĮą░ą╗ą░ąĘąĖ čüąĄ ą┐ąŠ čüą╗ąĄą┤ąĄčøąŠčś č乊čĆą╝čāą╗ąĖ:
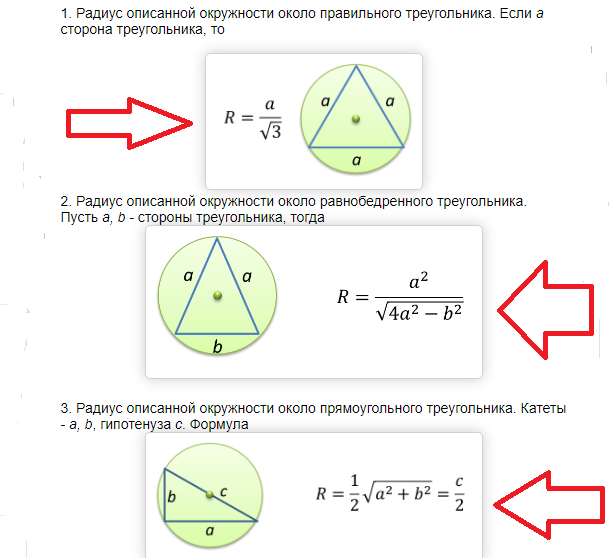
ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░:

ąĢą▓ąŠ čśąŠčł čśąĄą┤ąĮąŠą│ ą┐čĆąĖą╝ąĄčĆą░ čĆąĄčłą░ą▓ą░čÜą░ ą┐čĆąŠą▒ą╗ąĄą╝ ą║ąŠčĆąĖčłčøąĄčÜą░ ąźąĄčĆąŠąĮąŠą▓ąĄ č乊čĆą╝čāą╗ąĄ.
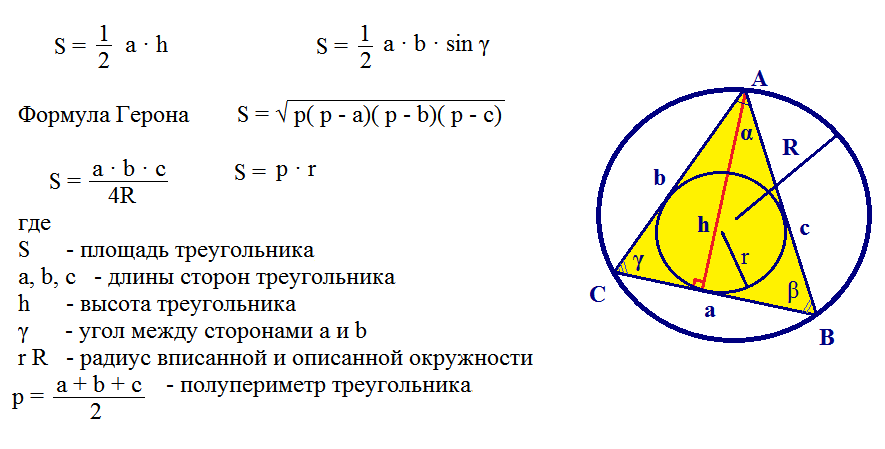
ąóąĄčłą║ąŠ čśąĄ čĆąĄčłąĖčéąĖ čüą╗ąĖčćąĮąĖ ą┐čĆąŠą▒ą╗ąĄą╝ąĖ, ą░ą╗ąĖ ąŠąĮąĖ čüąĄ ą╝ąŠą│čā ą┐čĆąĄą▓ą░ąĘąĖčøąĖ ą░ą║ąŠ ąĘąĮą░č鹥 čüą▓ąĄ č乊čĆą╝čāą╗ąĄ. ąóą░ą║ą▓ąĄ ąĘą░ą┤ą░čéą║ąĄ čāč湥ąĮąĖčåąĖ čĆąĄčłą░ą▓ą░čśčā čā 9. čĆą░ąĘčĆąĄą┤čā.
ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą░ąŠąĮąĖ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆą░ą┐ąĄąĘ: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ą┐čĆąŠą▒ą╗ąĄą╝ą░
ąØą░ ą┐čĆąĖą╝ąĄčĆ, čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆą░ą┐ąĄąĘ čśąĄ čāą┐ąĖčüą░ąĮ čüą░ ą║čĆčāą│ ą║ąŠčśąĖ čüąĄ ąĮą░ą╗ą░ąĘąĖ čā čéą░čćą║ąĖ ą┤ąŠą┤ąĖčĆą░ ą┤ąĄą╗ąĖ čśąĄą┤ąĮčā čüčéčĆą░ąĮčā ąĮą░ čüąĄą│ą╝ąĄąĮč鹥 ą╝ ąĖ ąĮ.
ąöą░ ą▒ąĖčüč鹥 čĆąĄčłąĖą╗ąĖ ąŠą▓ą░čś ą┐čĆąŠą▒ą╗ąĄą╝, ą┐ąŠčéčĆąĄą▒ąĮąŠ čśąĄ ą┤ą░ ą║ąŠčĆąĖčüčéąĖč鹥 čüą╗ąĄą┤ąĄčøąĄ č乊čĆą╝čāą╗ąĄ:

ą¤čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ čāą┐ąĖčüą░ąĮąŠą│ čā ą┐čĆą░ą▓ąŠčāą│ą░ąŠąĮąĖ čéčĆą░ą┐ąĄąĘ ą▓čĆčłąĖ čüąĄ ą┐čĆąĄą╝ą░ čüą╗ąĄą┤ąĄčøąŠčś č乊čĆą╝čāą╗ąĖ:
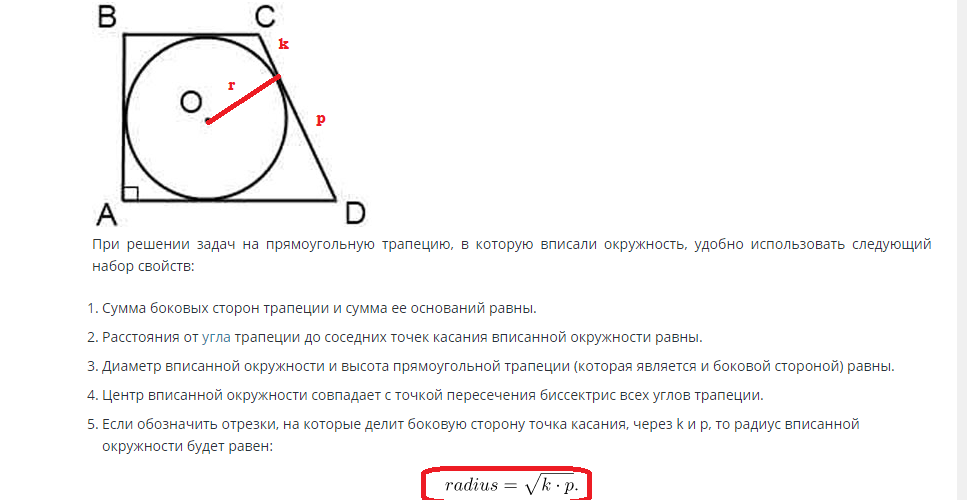
ąÉą║ąŠ čśąĄ ą┐ąŠąĘąĮą░čéą░ čüčéčĆą░ąĮąĖčåą░, ąŠąĮą┤ą░ čüąĄ ą┐čĆąĄą║ąŠ ąŠą▓ąĄ ą▓čĆąĄą┤ąĮąŠčüčéąĖ ą╝ąŠąČąĄ ąĮą░čøąĖ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║. ąÆąĖčüąĖąĮą░ čüčéčĆą░ąĮąĖčåąĄ čéčĆą░ą┐ąĄąĘą░ čśąĄą┤ąĮą░ą║ą░ čśąĄ ą┐čĆąĄčćąĮąĖą║čā ą║čĆčāą│ą░, ą░ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ čśąĄ ą┐ąŠą╗ą░ ą┐čĆąĄčćąĮąĖą║ą░. ąĪčģąŠą┤ąĮąŠ č鹊ą╝ąĄ, čĆą░ą┤ąĖčśčāčü čśąĄ čśąĄą┤ąĮą░ą║ ąĀ=ą┤/2.
ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░:

ą¤ąŠą▓čĆčłąĖąĮą░ ą║čĆčāąČąĮąĖčåąĄ ąŠą┐ąĖčüą░ąĮąĄ ąŠą║ąŠ ą┐čĆą░ą▓ąŠčāą│ą╗ąŠą│ ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą│ čéčĆą░ą┐ąĄąĘą░: č乊čĆą╝čāą╗ą░, ą┐čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ą┐čĆąŠą▒ą╗ąĄą╝ą░
ąóčĆą░ą┐ąĄąĘ čüąĄ ą╝ąŠąČąĄ čāą┐ąĖčüą░čéąĖ čā ą║čĆčāą│čā ą║ą░ą┤ą░ čśąĄ ąĘą▒ąĖčĆ čüčāą┐čĆąŠčéąĮąĖčģ čāą│ą╗ąŠą▓ą░ 180┬░. ąöą░ą║ą╗ąĄ, ą╝ąŠąČąĄ čüąĄ čāą┐ąĖčüą░čéąĖ čüą░ą╝ąŠ čśąĄą┤ąĮą░ą║ąŠčüčéčĆą░ąĮąĖčćąĮąĖ čéčĆą░ą┐ąĄąĘ. ą¤ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ąĘą░ ąĖąĘčĆą░čćčāąĮą░ą▓ą░čÜąĄ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ąŠą┐ąĖčüą░ąĮąŠą│ čā ą▒ą╗ąĖąĘąĖąĮąĖ ą┐čĆą░ą▓ąŠčāą│ą░ąŠąĮąŠą│ ąĖą╗ąĖ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąŠą│ čéčĆą░ą┐ąĄąĘą░ ąĖąĘčĆą░čćčāąĮą░ą▓ą░ čüąĄ ą┐ąŠą╝ąŠčøčā čüą╗ąĄą┤ąĄčøąĖčģ č乊čĆą╝čāą╗ą░:

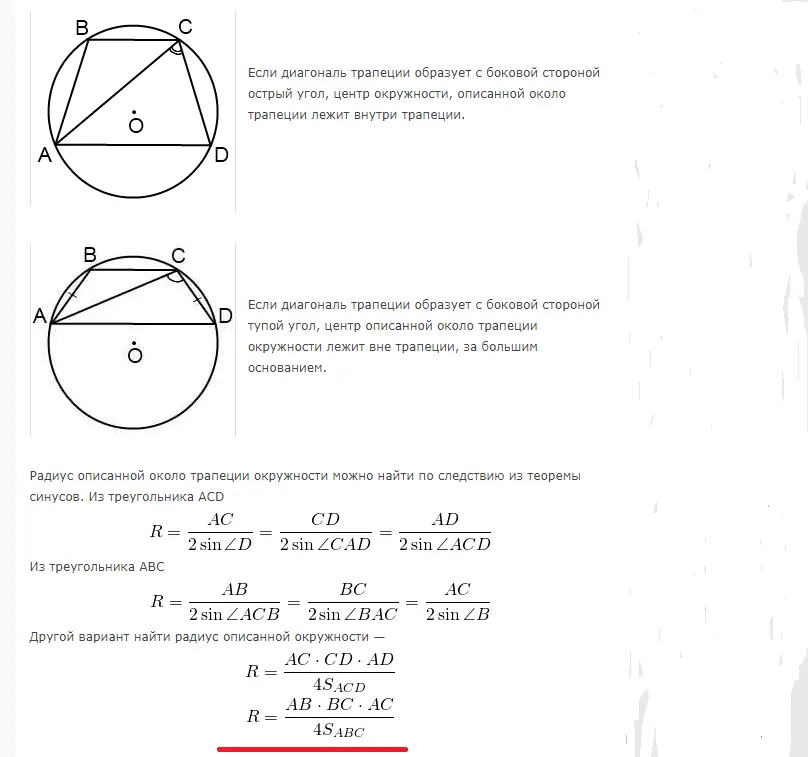
ą¤čĆąĖą╝ąĄčĆąĖ čĆąĄčłą░ą▓ą░čÜą░ ąĘą░ą┤ą░čéą░ą║ą░:
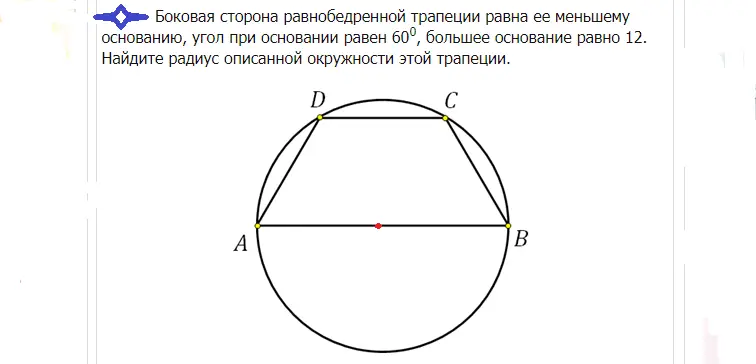
ąĀąĄčłąĄčÜąĄ: ąÆąĄą╗ąĖą║ą░ ą▒ą░ąĘą░ čā ąŠą▓ąŠą╝ čüą╗čāčćą░čśčā ą┐čĆąŠą╗ą░ąĘąĖ ą║čĆąŠąĘ čåąĄąĮčéą░čĆ, ą┐ąŠčłč鹊 čśąĄ čśąĄą┤ąĮą░ą║ąŠą║čĆą░ą║ąĖ čéčĆą░ą┐ąĄąĘ čāą┐ąĖčüą░ąĮ čā ą║čĆčāą│. ą”ąĄąĮčéą░čĆ ą┤ąĄą╗ąĖ ąŠą▓čā ą▒ą░ąĘčā čéą░čćąĮąŠ ąĮą░ ą┐ąŠą╗ą░. ąÉą║ąŠ čśąĄ ąŠčüąĮąŠą▓ą░ ąÉąæ čśąĄą┤ąĮą░ą║ą░ 12, ąŠąĮą┤ą░ čüąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ ąĀ ą╝ąŠąČąĄ ąĮą░čøąĖ ąĮą░ čüą╗ąĄą┤ąĄčøąĖ ąĮą░čćąĖąĮ: ąĀ=12/2=6.
ą×ą┤ą│ąŠą▓ąŠčĆ: ą¤ąŠą╗čāą┐čĆąĄčćąĮąĖą║ čśąĄ 6.
ąŻ ą│ąĄąŠą╝ąĄčéčĆąĖčśąĖ čśąĄ ą▓ą░ąČąĮąŠ ąĘąĮą░čéąĖ č乊čĆą╝čāą╗ąĄ. ąÉą╗ąĖ ąĮąĄą╝ąŠą│čāčøąĄ čśąĄ ąĘą░ą┐ą░ą╝čéąĖčéąĖ čüą▓ąĄ čÜąĖčģ, ą┐ą░ čśąĄ čćą░ą║ ąĖ ąĮą░ ą╝ąĮąŠą│ąĖą╝ ąĖčüą┐ąĖčéąĖą╝ą░ ą┤ąŠąĘą▓ąŠčÖąĄąĮąŠ ą║ąŠčĆąĖčüčéąĖčéąĖ ą┐ąŠčüąĄą▒ą░ąĮ ąŠą▒čĆą░ąĘą░čå. ą£ąĄčÆčāčéąĖą╝, ą▓ą░ąČąĮąŠ čśąĄ ą┐čĆąŠąĮą░čøąĖ ą┐čĆą░ą▓čā č乊čĆą╝čāą╗čā ąĘą░ čĆąĄčłą░ą▓ą░čÜąĄ ąŠą▓ąŠą│ ąĖą╗ąĖ ąŠąĮąŠą│ ą┐čĆąŠą▒ą╗ąĄą╝ą░. ąÆąĄąČą▒ą░čśč鹥 čĆąĄčłą░ą▓ą░čÜąĄ čĆą░ąĘą╗ąĖčćąĖčéąĖčģ ąĘą░ą┤ą░čéą░ą║ą░ ąĘą░ ą┐čĆąŠąĮą░ą╗ą░ąČąĄčÜąĄ ą┐ąŠą╗čāą┐čĆąĄčćąĮąĖą║ą░ ąĖ ą┐ąŠą▓čĆčłąĖąĮąĄ ą║čĆčāą│ą░ ą║ą░ą║ąŠ ą▒ąĖčüč鹥 ą╝ąŠą│ą╗ąĖ ą┐čĆą░ą▓ąĖą╗ąĮąŠ ąĘą░ą╝ąĄąĮąĖčéąĖ č乊čĆą╝čāą╗ąĄ ąĖ ą┤ąŠą▒ąĖčéąĖ čéą░čćąĮąĄ ąŠą┤ą│ąŠą▓ąŠčĆąĄ.















