Формула времена, брзине и удаљености: 4. разред. Како пронаћи време, знајући брзину и раздаљину? Како пронаћи брзину ако су време и растојање познати? Како пронаћи растојање ако су време и брзина познати? Графикон зависности брзине тела од времена

Како решити задатке кретања? Формула за однос између брзине, времена и удаљености. Задаци и решења.

Формула за зависност времена, брзине и удаљености за 4. разред: како се означава брзина, време, растојање?

Људи, животиње или машине могу да се крећу одређеном брзином. Они могу ићи одређеним путем у одређено време. На пример: данас можете стићи у школу за пола сата. Ходате одређеном брзином и пређете 1000 метара за 30 минута. У математици се пут који се савлада означава словомС. Брзина се означава словом в. А време за које је пут пређен означава се словом т.

• Пут —С
• Брзина — в
• Време —т

Ако закасните у школу, може исто проћи пут за 20 минута, повећавајући своју брзину. То значи да се исти пут може прећи у различито време и различитим брзинама.

Како време путовања зависи од брзине?

Што је већа брзина, брже ће се прећи пут. И што је мања брзина, дуже ће бити потребно да се заврши путовање.

​​

Како пронаћи време знајући брзину и раздаљину?

Да бисте пронашли време потребно за прелазак једне удаљености, морате знати растојање и брзину. Ако раздаљину поделите са брзином, знаћете време. Пример таквог задатка:

Задатак о зецу. Зец је побегао од Вука брзином од 1 километар у минуту. Трчао је 3 километра до своје рупе. После неког времена Харе је отрчао у рупу?

Колико је лако решити проблеме кретања где треба да пронађете растојање, време или брзину?

1. Пажљиво прочитајте задатак и одредите шта је познато из услова задатка.
2. Упишите ове податке на нацрт.
3. Такође напишите шта је непознато и шта се може наћи
4. Користите формулу за проблеме удаљености, времена и брзине
5. Унесите познате податке у формули и решити задатак

Решење задатка о зецу и вуку.

• Из услова задатка утврђујемо да знамо брзину и растојање.
• Такође из услова задатка утврђујемо да треба да нађемо време које је зецу било потребно да отрчи до рупе.

Ове податке уписујемо у нацрт, на пример:

Удаљеност до рупе — 3 километра

Брзина зеца — 1 километар за 1 минут

Време је непознато

Хајде да то исто запишемо математичким симболима:

С— 3 километра

В — 1 км/мин

т—?

Подсећамо се и записујемо формулу за проналажење времена у свесци:

т = С: в

Сада записујемо решење задатка бројевима:

т = 3: 1 = 3 минута

Како пронаћи брзину ако су познати време и растојање?

Да би се пронашла брзина, ако су време и растојање познати, растојање се мора поделити са временом. Пример таквог задатка:

Зец је побегао од Вука и отрчао 3 километра до његове рупе. Прешао је ову удаљеност за 3 минута. Колико брзо је Зец трчао?

Решење задатка кретања:

1. У нацрту пишемо да знамо растојање и време.
2. Из услова задатка утврђујемо да треба пронаћи брзину
3. Подсећамо се на формулу за налажење брзине.

Формуле за решавање оваквих проблема су приказане на слици испод.

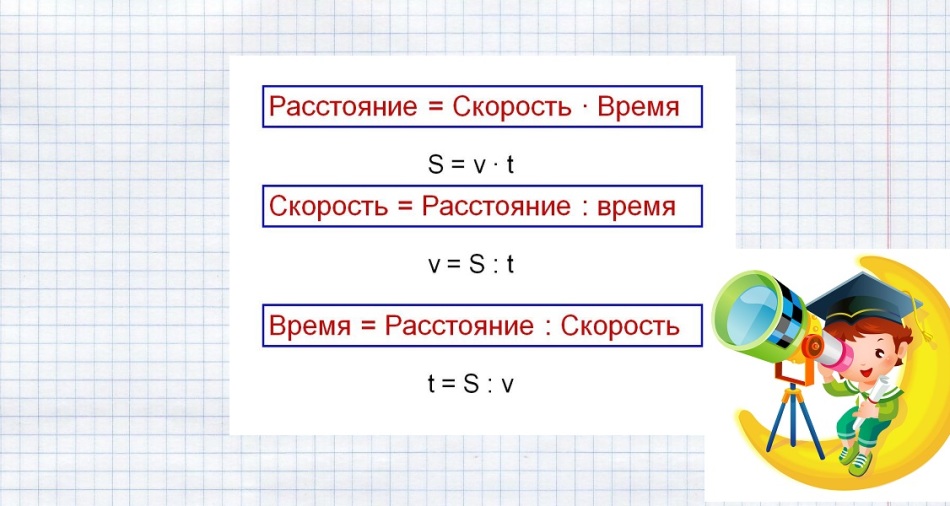
Замените познате податке и решите задатак:

Удаљеност до рупе је 3 километра

Време које је Зецу требало да стигне до рупе било је 3 минута

Брзина је непозната

Запишимо ове познате податке математичким симболима

С— 3 километра

 т— 3 минута

в —?

Записујемо формулу за проналажење брзине

в = С: т

Сада записујемо решење задатка бројевима:

в = 3: 3 = 1 км/мин

Како пронаћи растојање ако је време а брзина се зна?

Да бисте пронашли растојање, ако су време и брзина познати, помножите са брзином. Пример таквог задатка:

Зец је побегао од Вука брзином од 1 километра за 1 минут. Требало му је три минута да отрчи до рупе. Колико је Зец претрчао?

Решење задатка: У нацрт уписујемо оно што знамо из услова задатка:

Брзина Зеца је 1 километар за 1 минут

Време када је Зец отрчао до рупе - 3 минута

Удаљеност - непознато

Хајде да запишемо исто математичким симболима:

в — 1 км/мин

т— 3 минута

С —?

Подсећамо се формуле за проналажење растојања:

С = в ⋅ т

Сада записујемо решење задатка бројевима:

С = 3 ⋅ 1 = 3 км

Како научити да решавате сложеније задатке?

Да бисте научили како да решавате сложеније задатке, морате да разумете како да решавате једноставне, запамтите који знаци означавају растојање, брзину и време. Ако не можете да се сетите математичких формула, запишите их на комад папира и увек их држите при руци приликом решавања задатака. Са дететом решавајте једноставне задатке које можете смислити у покрету, на пример, током шетње.

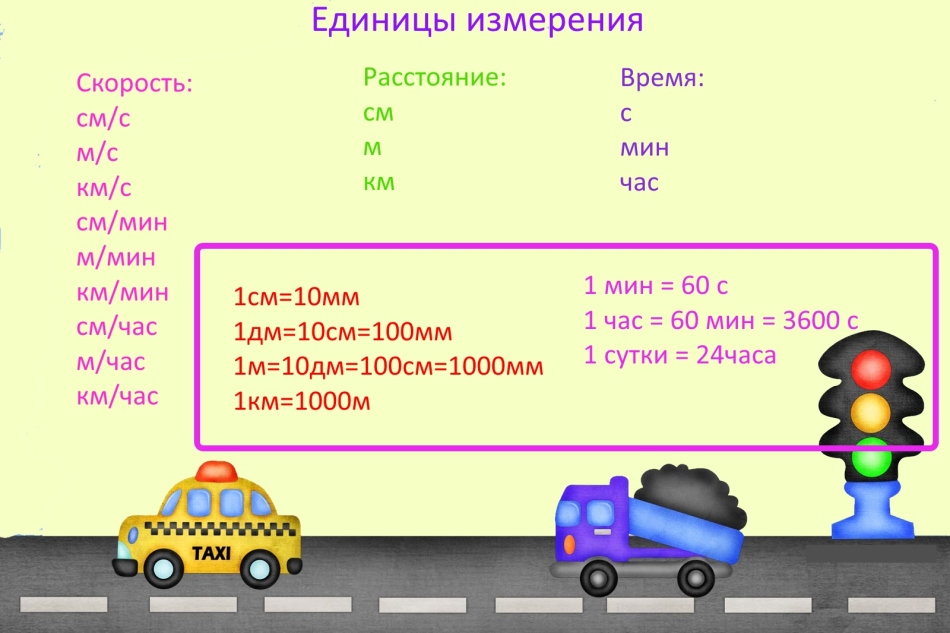
Јединице мере

Приликом решавања задатака о брзини, времену и удаљености често греше јер забораве да конвертују мерне јединице.

ВАЖНО: Јединице мере могу бити било које, али ако постоје различите мерне јединице у истом задатку, претворите их у исте. На пример, ако се брзина мери у километрима у минути, онда се растојање мора приказати у километрима, а време у минутима.

За радознале : Општеприхваћени систем мера назива се метрички, али то није увек био случај, а у старој Русији су се користиле друге мерне јединице.

Проблем Боа : Слончић и мајмун измерили су дужину боа у корацима. Кретали су се једно према другом. Брзина мајмуна је била 60 цм у једној секунди, а брзина бебе слона 20 цм у једној секунди. На мерење су потрошили 5 секунди. Колика је дужина боа? (решење испод слике)

&лт;&гт; Решење:

Из услова задатка утврђујемо да знамо брзину мајмуна и бебе слона и време које им је потребно да измере дужину удава.

Запишимо ове податке:

Брзина мајмуна је 60 цм/сец

Брзина бебе слона је 20 цм/сек

Време — 5 секунди

Непознато растојање

Запишимо ове податке математичким симболима:

в1 — 60 цм/сец

в2 — 20 цм/сец

т — 5 секунди

С —?

Хајде да запишемо формулу за растојање, ако су брзина и време познати:

С = в ⋅ т

Избројимо удаљеност коју је прешао мајмун:

С1 = 60 ⋅ 5 = 300 цм

Хајде сада да избројимо колико је слон прешао:

С2 = 20 ⋅ 5 = 100 цм

Сабирамо пут који је прешао мајмун и пут који је прешао слон:

С = С1 + С2 = 300 + 100 = 400 цм

График зависности брзине тела од времена: фотографија

Растојање покривено различитим брзинама покривено је у различито време. Што је већа брзина, то је мање времена потребно за кретање.

Табела 4 класа: брзина, време, растојање

Бр.	Брзина (км/х)	Време (сат)	Растојање (км)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Можете маштати и смислити задатке за сами сто. Испод су наше опције за услове задатака:

1. Мама је послала Црвенкапицу баки. Девојчица је била стално расејана и ходала је кроз шуму полако, брзином од 5 км/х. На путу је провела 2 сата. Колико је далеко прешла Црвенкапа за то време?
2. Поштар Печкин је носио пакет на бициклу брзином од 12 км/х. Он зна да је растојање између његове куће и куће стрица Федора 12 км. Помозите Печкину да израчуна колико ће времена бити потребно за путовање?
3. Папа Ксјуша је купио ауто и одлучио да одведе породицу на море. Аутомобил се кретао брзином од 60 км/х и на путу је провео 4 сата. Колика је удаљеност између Ксјушине куће и морске обале?
4. Патке су се скупиле у клин и одлетеле у топле крајеве. Птице су неуморно махале крилима 3 сата и за то време прешле 300 км. Која је била брзина птица?
5. Авион АН-2 лети брзином од 220 км/х. Полетео је из Москве и лети за Нижњи Новгород, растојање између ова два града је 440 км. Колико дуго ће авион бити на путу?

Одговоре на дате задатке можете пронаћи у табели испод:

Бр.	Брзина (км/х)	Време (сат)	Растојање (км)
1	5	2	10
2	12	1]	12
3	60	4	240
4	100	3	300
5	220	2	440

Примери решавања задатака брзине, времена, удаљености за 4. разред

Ако се у једном задатку налази више објеката у покрету, потребно је да научите дете да разматра кретање ових предмета одвојено, а тек онда заједно. Пример таквог задатка:

Два пријатеља Вадик и Тема одлучили су да прошетају и напустили су своје куће да се сретну. Вадик је возио бицикл, а Тема је ходала. Вадик је возио брзином од 10 км/х, а Тема је ишао брзином од 5 км на сат. Сат касније срели су се. Колика је удаљеност између кућа Вадик и Тема?

Овај проблем се може решити коришћењем формуле за зависност удаљености од брзине и времена.

С = в ⋅ т

Удаљеност коју Вадик пређе на бициклу биће једнака његовој брзини помноженој по времену у транзиту.

С = 10 ⋅ 1 = 10 километара

Путање које је Субјект прешао израчунава се на сличан начин:

С = в ⋅ т

Замените дигиталне вредности његове брзине и времена у формулу

С = 5 ⋅ 1 = 5 километара

Раздаљина коју је прешао Вадик мора се додати раздаљини коју је прешао Тема.

10 + 5 = 15 километара

Како научити да решавате сложене проблеме који захтевају логичко размишљање?

За развој логичког мишљења детета потребно је из њих решавати једноставне, па сложене логичке задатке. Ови задаци се могу састојати од неколико фаза. Можете прећи из једне фазе у другу само ако је претходна решена. Пример таквог задатка:

Антон је возио бицикл брзином од 12 км/х, а Лиза је возила скутер брзином 2 пута мањом од Антонове, а Денис ходао брзином 2 пута мањом од Лизине. Која је брзина Дениса?

Да бисте решили овај проблем, морате прво знати Лизину брзину, а тек онда Денисову брзину.

Два бициклиста су кренула из различитих градова да се сретну. Један од њих је журио и јурио је брзином од 12 км/х, а други је лагано возио брзином од 8 км/х. Удаљеност између градова из којих су бициклисти кренули је 60 км. Колико ће сваки бициклиста прећи пре него што се сретну? (решење испод фотографије)

Решење:

• 12+8 = 20 (км/х) је укупна брзина два бициклиста, или брзина којом су се приближили један другом
• 60: 20 = 3 (х) је време након којег су се бициклисти срели
• 3 ⋅ 8 = 24 (км) је пут који је прешао први бициклиста
• 12 ⋅ 3 = 36 (км) је пут који је прешао други бициклиста
• Проверите: 36+24=60 (км) је пут који су превалила два бициклиста.
• Одговор: 24 км, 36 км.

Понудите деци да реше следеће задатке у виду игре. Можда ће желети да направе свој проблем о пријатељима, животињама или птицама.

ВИДЕО: Проблеми са кретањем